Conway's Game Of Life
Posted August 6th, 2019
Cellular Automata
A cellular automaton is a model that is made up of a grid of cells, each cell has a specific state.
The grid is configured with an initial state, and every generation the state of the cells change depending on the states of the surrounding (neighbouring) cells.
Cellular automata have been used to model all sorts of things. John von Neumann used this to model a self replicating machine (known as a universal constructor). His universal constructor uses a cellular automaton that has a two dimensional grid of cells, each cell can have one of 29 states.
His machine would read from a "tape" to produce another machine, then copy the that tape, so that machine can be copied again.
He did all of this before Watson and Crick discovered the structure of DNA.
Conway's Game Of Life
The cellular automaton I'll implement in this article is much simpler than the universal constructor, but that doesn't mean it isn't interesting.
It works like this:
- Each cell has one of two states. You can think of this as populated vs unpopulated.
- Every generation, the state of a cell changes on how many neighbours are populated:
- A cell "dies" if has fewer than two or more than three neighbours.
- A cell becomes populated if it has three neighbours.
- Otherwise, if a cell has two neighbours, it remains in stasis.
Whilst these rules are simple, many complex things can emerge from these simple rules. Here is what I am going to make in this article:

Setup
I'll make a file called index.html. This will have a canvas element and a script tag so we can get started.
<!DOCTYPE html>
<html>
<head>
<title>Game Of Life</title>
</head>
<body>
<canvas width="720" height="480" id="canvas">
</canvas>
<script type="text/javascript">
</script>
<style type="text/css">
canvas {
border: thin solid black;
}
</style>
</body>
</html>Populating The Grid
We need to create the grid of cells. We'll do this by creating a two dimensional array.
var canvas = document.getElementById("canvas");
var ctx = canvas.getContext("2d");
var cellSize = 10;
var numRows = Math.floor(canvas.height/cellSize);
var numCols = Math.floor(canvas.width/cellSize);
var cells = Array.from(Array(numRows), () => new Array(numCols));I will add a utility method to Array to simplify iteration through a two dimensional array. And use this to randomly set the states of the cells.
1 will represent populated, and 0 will represent unpopulated.
Array.prototype.loop2d = function(callback) {
for (var row = 0; row < this.length; row++)
for (var col = 0; col < this[row].length; col++)
callback(this[row][col], row, col);
};
cells.loop2d((element, row, col) => cells[row][col] = (Math.random() * 100 < 60) ? 1 : 0);Now we'll render the grid. Populated cells are white, unpopulated cells are black.
drawGrid();
function drawGrid() {
cells.loop2d((element, row, col) => {
ctx.fillStyle = element == 0 ? 'black' : 'white';
ctx.fillRect(col*cellSize, row*cellSize, cellSize, cellSize);
}) ;
}We should get something like this:

Simulate
Now we will simulate one generation. This will take in the current grid of cells, and return a new one. This is so that changing the state of the cell doesn't change the others in the same generation, that's why we need a copy.
function simulate(cells) {
var newCells = Array.from(Array(numRows), () => new Array(numCols));
newCells.loop2d((element, row, column) => newCells[row][column] = 0);
return newCells;
}Then I iterate though it. I can't use loop2d to iterate because not all cells have neighbours, so we will leave out the first and last rows and columns. By default the cells will be initialised to unpopulated.
function simulate(cells) {
var newCells = Array.from(Array(numRows), () => new Array(numCols));
newCells.loop2d((element, row, column) => newCells[row][column] = 0);
for (var row = 1; row < cells.length-1; row++) {
for (var col=1; col < cells[row].length; col++) {
}
}
return newCells;
}Now we need to count the number of neighbours by iterating through each cell and looping through neighbouring elements.
for (var row = 1; row < cells.length-1; row++) {
for (var col=1; col < cells[row].length; col++) {
var numNeighbours = 0;
for (var i = -1; i < 2; i++) {
for (var j = -1; j < 2; j++) {
numNeighbours += cells[row+i][col+j] == 1 ? 1 : 0;
}
}
}
}Since we don't want to count the current cell as a neighbour, we have to subtract it from the number of neighbours.
for (var row = 1; row < cells.length-1; row++) {
for (var col=1; col < cells[row].length; col++) {
var numNeighbours = -cells[row][col];
for (var i = -1; i < 2; i++) {
for (var j = -1; j < 2; j++) {
numNeighbours += cells[row+i][col+j] == 1 ? 1 : 0;
}
}
}
}And now for the important part, setting the new state depending on the number of neighbours. Since it is initialised to zero, the only time it will change is if it has three neighbours, or if it is in statis and has a state of populated.
for (var row = 1; row < cells.length-1; row++) {
for (var col=1; col < cells[row].length; col++) {
var numNeighbours = 0;
var numNeighbours = -cells[row][col];
for (var i = -1; i < 2; i++) {
for (var j = -1; j < 2; j++) {
numNeighbours += cells[row+i][col+j] == 1 ? 1 : 0;
}
}
if (numNeighbours==2) newCells[row][col] = cells[row][col];
if (numNeighbours==3) newCells[row][col] = 1;
}
}Now I will simulate one generation.
cells.loop2d((element, row, col) => cells[row][col] = (Math.random() * 100 < 60) ? 1 : 0);
drawGrid();
cells = simulate(cells);
drawGrid();There should be a noticable difference between the initial random state and the current one:
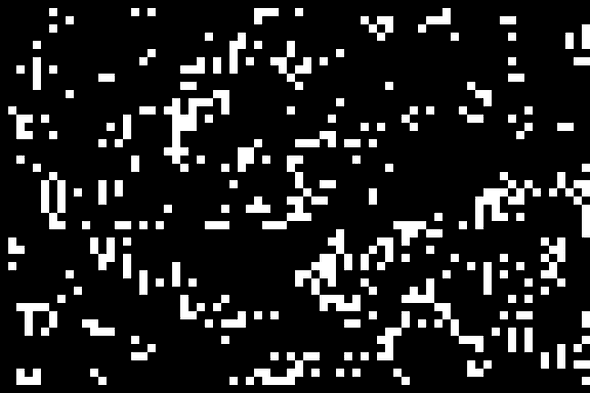
And now we will simulate a generation every 32 milliseconds.
cells.loop2d((element, row, col) => cells[row][col] = (Math.random() * 100 < 60) ? 1 : 0);
drawGrid();
setInterval(() => {
cells = simulate(cells);
drawGrid();
}, 32);Patterns
A number of patterns emerge from Conway's game of life. Three of the most common types of patterns are:
- Still lifes. Think of a 2x2 square, these don't change (without outside contact).
- Oscillators. These repeat after a certain number of generations. A line of three cells is a good example.
- Spaceships. These move across the screen.
Many of these configurations eventually stabilise, but some grow forever. I've set the intial configuration randomly, but usually people try to achieve one of these infinite patterns by directly specifying the initial states.
Try extending this by coming up with such initial patterns.