Separating Axis Theorem Collision Detection
Posted May 25th, 2021
Introduction
In a game you often have to check if two things are colliding. Maybe the player enters a zone that triggers a cutscene. Or maybe they shoot a projectile at an enemy. At some point you probably have to detect if two objects are colliding, and respond appropriately.
How you check for a collision and respond to it depends on the shape of the objects that collide.
You might want to check if two circles are colliding. In that case, you use Pythagoras's theorem to get the distance between them and check if it is smaller than the sum of the radii.
Or maybe you want to check a collision for two "axis-aligned" rectangles. In that case you check for overlap along the x-axis and the y-axis.
In this article I will describe how to check for a collision between "oriented" rectangles and polygons using a method known as "The Separating Axis Theorem" (SAT).
There are many articles about this online, but it took me a while to understand. In this post I will try to make this as intuitive as possible, and show how it can be implemented in code. To get there, I will start by showing how it is an extension of fairly simple collision detection methods.
Guess The Number
I will start with something very simple. I have a random number, I want to check if a guess is the same as the number. You can think of this as the guess and the number occupying the same location in 1D space.
In code it would look something like this:
function checkGuess(num: number, guess: number): Boolean {
return num === guess
}You Sunk My Battleship!
Lets extend the previous example a little. Imagine a one dimensional version of battleships, where there is one ship with a starting position and a "width". How can we check if a tile position is intersecting with the ship?
To make this work, we have to check that the the guess is between the position of the start of the ship and the position at the end of the ship.
In code it would look like something like this:
function isBetween(num: number, min: number, max: number): Boolean {
return number >= min && number <= max
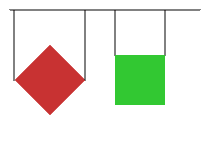
}What if the projectile fired at the battleship is wider than one unit? How would we check if they are colliding?
If one of the maximum points is less than the other minimum point, then they can't be colliding. Otherwise, we can assume that they are. Here is a visualisation:
As you can see, the minimum point of the green rectangle is greater than the maximum point of the red rectangle. You could draw a line between the two rectangles.
function overlaps(
aMin: number,
aMax: number,
bMin: number,
bMax: number
): Boolean {
return aMax >= bMin && aMin <= bMax
}The examples so far may seem trivial, but they are actually what the SAT reduces to. The only difference is that we have to do some computation to get the positions and we have to do it for more than one dimension. A loop and a function call, to get from here to there.
Axis Aligned Bounding Boxes
The next step is detecting collision for "axis aligned" rectangles (AABBs). This means non-rotated rectangles. This is just like the previous example, but there are 2 dimensions rather than 1. You have to detect for collision on the x-axis and the y-axis.
Here is how we might represent an AABB:
class Rectangle {
x: number
y: number
width: number
height: number
constructor(x: number, y: number, width: number, height: number) {
this.x = x
this.y = y
this.width = width
this.height = height
}
}Just like before, we can calculate the min positions using the position and the max position using the min position plus the size. After that, we can use the same method for detecting overlap:
isColliding(other: Rectangle) : Boolean {
return overlaps(this.x, this.x + this.width, other.x, other.x + other.width) &&
overlaps(this.y, this.y + this.height, other.y, other.y + other.height)
}If one of the axis don't have an overlap, then they aren't colliding. Take the battelships visualisation above. If we treat it like it is 2D, then we can say that it is intersecting along the y-axis but not the x-axis. This will be important when we deal with objects that are not axis-aligned.
Oriented bounded boxes
The difference between detecting collision for an AABB and a OBB is that we can't assume the sides are perfectly aligned with the x and y-axis.
This means that rather than getting x and y coordinates and sizes, we have to calculate the distances along each axis on the shape. We can do this using dot products. More on this later. First, a visualisation:
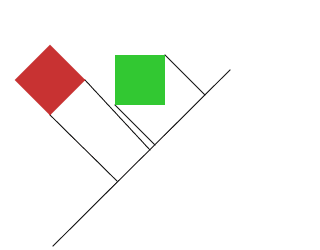
One of the rectangles is Axis Aligned. We want to know if they collide along the x-axis, so we need to find the minimum and maximum x-positions on both rectangles, and see if they overlap. To do this we just need to find the corners with the smallest and largest x coordinates.
But we also need to check all of the axes. And since it's not axis aligned, that means we have to check for the other faces, e.g the 45 degree angle:
Let's call this 45 degree line the Q-axis. We could say that the red rectangle has a minimum and maximum Q position, and so does the green one. And checking for overlap works the same way as it did for the x and y axis.
So how do we know how far along the Q axis a point is?
As mentioned above, dot products.
To explain how we can use dot products to solve this problem, I need to explain vectors:
First, a refresher on vector maths:
A vector is a mathematical object with a magnitude and a dimension. A 2 dimensional vector has to components, we can call this an x component and a y component. Technically they can't be used for coordinates, but for convenience's sake we will use it.
Vectors can have their components added and subtracted with each other, and support a few more operations but for now we will stick to these simple ones:
class Vector2f {
x: number
y: number
constructor(x = 0, y = 0) {
this.x = x
this.y = y
}
static add(left: Vector2f, right: Vector2f) {
return new Vector2f(left.x + right.x, left.y + right.y)
}
static subtract(left: Vector2f, right: Vector2f) {
return new Vector2f(left.x - right.x, left.y - right.y)
}
multiply(scale: number) {
return new Vector2f(this.x * scale, this.y * scale)
}
}A dot product checks how much two vectors are facing the same direction.
This is done by adding multiplying the x components of two vectors and adding that to the multiple of the y components:
dot(other: Vector2f) {
let vec1 = this;
let vec2 = other;
return vec1.x*vec2.x + vec1.y*vec2.y;
}If both vectors have the same signs for all components, all negative or all positive, then the result is a positive number. If both vectors have the same signs then in some sense they are pointing in the same direction.
If the vectors have different signs, then multiplying a negative number by a positive number gives a negative number.
And if one of the components is zero, then you get a dot product of zero.
You can use the dot product to find out how far along a point is across an axis, if the number is big then it is further along.
If we can tell how far along the axis a point is, then we do this calculation for all points, and check for overlap between the minimum and the maximum points.
To show this in code, I'll start with an oriented rectangle class:
class OrientedRectangle {
position: Vector2f
dimensions: Vector2f
centre: Vector2f
angle: number
constructor(position: Vector2f, dimensions: Vector2f, angle: number) {
this.position = position
this.dimensions = dimensions
this.angle = angle
this.centre = Vector2f.add(this.position, this.dimensions.multiply(0.5))
}
}Now let's make an isColliding function:
isColliding(other: OrientedRectangle) {
const axes = getAxes().concat(other.getAxes())
const corners = getCorners()
const otherCorners = other.getCorners()
for (axis of axes) {
}
}And now let's fill out the other functions we need before proceeding with this:
getAxes() : Array<Vector2f> {
// in a rectangle, opposite sides are parallel
// meaning that they face the same direction
// so there is no need to perform a dot product with the same vector twice
// one side is also 90 degrees shifted from the other
return [
new Vector2f(
Math.cos(toRadians(this.angle)),
Math.sin(toRadians(this.angle))
),
new Vector2f(
Math.cos(toRadians(90.0 + this.angle)),
Math.sin(toRadians(90.0 + this.angle))
)
]
}
// don't forget toRadians
function toRadians(num: number) {
return num * Math.PI / 180
}
Next is getCorners:
getCorners() {
// don't worry too much about how this works
// it assumes that the rectangle is located with a centre of (0, 0)
// then it rotates using complex numbers (multiply to rotate from real to imaginary numbers)
// (You can rotate using other methods)
// then it adds the rotated corners to the centre position
// giving the coordinates of all the coordinates
// this is mostly useful if the angle or position of the rectangle can change
// which is normally the case in games
const halfDimensions = this.dimensions.multiply(0.5)
return [
halfDimensions.multiply(-1),
new Vector2f(halfDimensions.x, -halfDimensions.y),
new Vector2f(-halfDimensions.x, halfDimensions.y),
halfDimensions
].map (point => {
const complexAngle = new Vector2f(
Math.cos(toRadians(this.angle)),
Math.sin(toRadians(this.angle))
)
return Vector2f.add(
new Vector2f(
point.x * complexAngle.x - point.y * complexAngle.y,
point.x * complexAngle.y + point.y * complexAngle.x
), this.centre)
})
}
Now let's flesh out the rest of the isColliding function:
isColliding(other: OrientedRectangle) {
const axes = this.getAxes().concat(other.getAxes())
const corners = this.getCorners()
const otherCorners = other.getCorners()
for (let axis of axes) {
const [thisMin, thisMax] = this.getMinVertex(axis, corners)
const [otherMin, otherMax] = this.getMinVertex(axis, otherCorners)
// if one of the axes does not overlap, it's not colliding
if (thisMax < otherMin || otherMax < thisMin) return false;
}
// none of the axes have overlapped, so it is colliding
return true;
}And now there is only one more function to fill out:
getMinVertex(axis: Vector2f, corners: Array<Vector2f>) {
let thisMin = corners[0].dot(axis)
let thisMax = thisMin
for (let corner of corners) {
const distance = corner.dot(axis)
if (distance < thisMin) thisMin = distance
if (distance > thisMax) thisMax = distance
}
return [thisMin, thisMax]
}And that's it! Most of the work was in getting the axes and getting the corners. I could have left that out and hardcoded it, but if you need to use the SAT for collision detection you probably also need code to do those things too.
Polygons
The same idea applies for polygons, but there are less assumptions we can make. For one, we can't assume that they have parallel sides. We also can't assume the number of sides or where they start. So we have to store the distance from every corner to the centre of the polygon, and the angle of the polygon. Then you have to loop through the corners and obtain the direction from the previous to the next corner to get the axis.
But once you have represented the corners, checking for collision is exactly the same.
Next Steps
Usually detecing whether or not two objects are colliding is not enough for a game. Collisions often have to be resolved in some way. And to resolve these collisions, more information is often needed about the collision. What direction are they moving relative to eachother? How much are they colliding? Is the collision being resolved? What faces are involved in the collision?
And finally, after this, they can be dealt with in various ways. Often this involves "elastic collision". Like the name implies, it means they bounce with the right amount of force. Collisions often have angular effects.
This will be the focus of a future article, where I will use Sutherland Hodge clipping to get information about the collision face, and use simple kinematics to make the polygons bounce.